Simulation Convergence Whitepaper and DLL Action Tree
Whitepaper - Monte Carlo Simulation Convergence
How fast can you get reliable results?
How many samples should I run? This is the first question users always ask when they run a Monte Carlo simulation. The answer could be complicated, but the simple rule is that you need to run the number of samples until your designated goals (such as the descriptive statistic of measurements) are not affected by changing the number of samples.
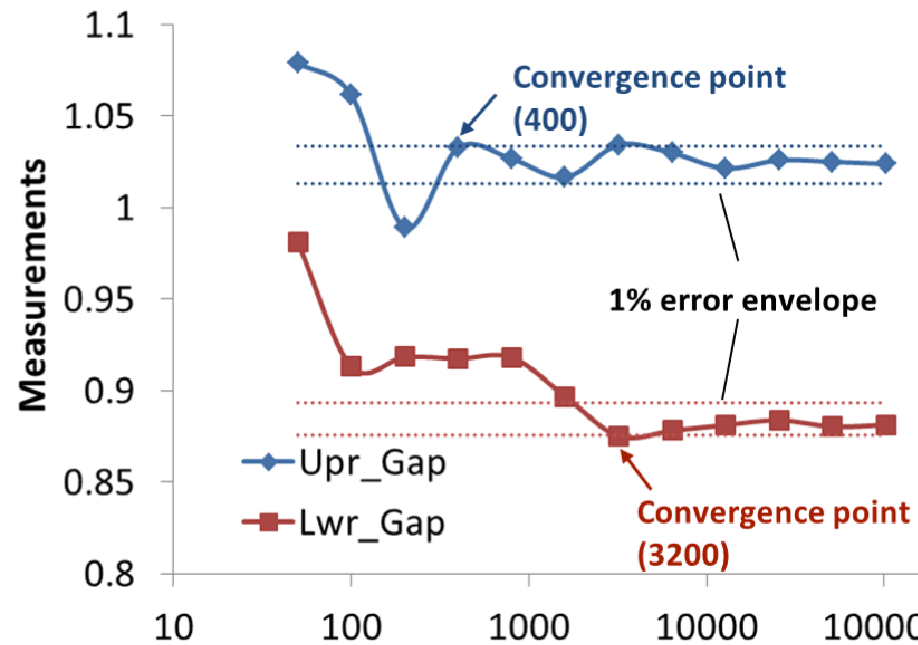
3DCS convergence utility recommends the required number of simulation samples to make measurements converge to a confidence interval. This utility is model-independent and only requires selecting confidence level and percent error within the standard deviation. The strategy is developed based on convergence of standard deviation using Chi-squared test for variance in a normal population. The fundamental of the method is elaborated in Convergence Strategy Section. The convergence study in 3DCS Monte Carle simulation shows that this convergence strategy works well for the most common type of measurements and the single-contributor measurements, although it overestimates for the equation measurements which introduce more nonlinearity and volatility into the model.
In the current version, it is designed to give users suggestion about how many samples they should run in 3DCS Monte Carlo simulations. It is model independent and easy to use; however, it relies on some assumptions and overestimates certain cases. As such, DCS plans to develop this utility further. More convergence criteria could be added, such as mean value. Convergence process curves may be added to assist the user to determine if the measurements are converged. These advancements are expected in the future releases of 3DCS.
Fill out the Form to the right to download the Whitepaper and DLL Action Tree -->
DLL Action Trees
Helpful Tools for Applying DLL's in 3DCS
Simulation Convergence
Measurements of the upper gap and the lower gap vs. the number of simulation samples
What is 3DCS Variation Analyst?
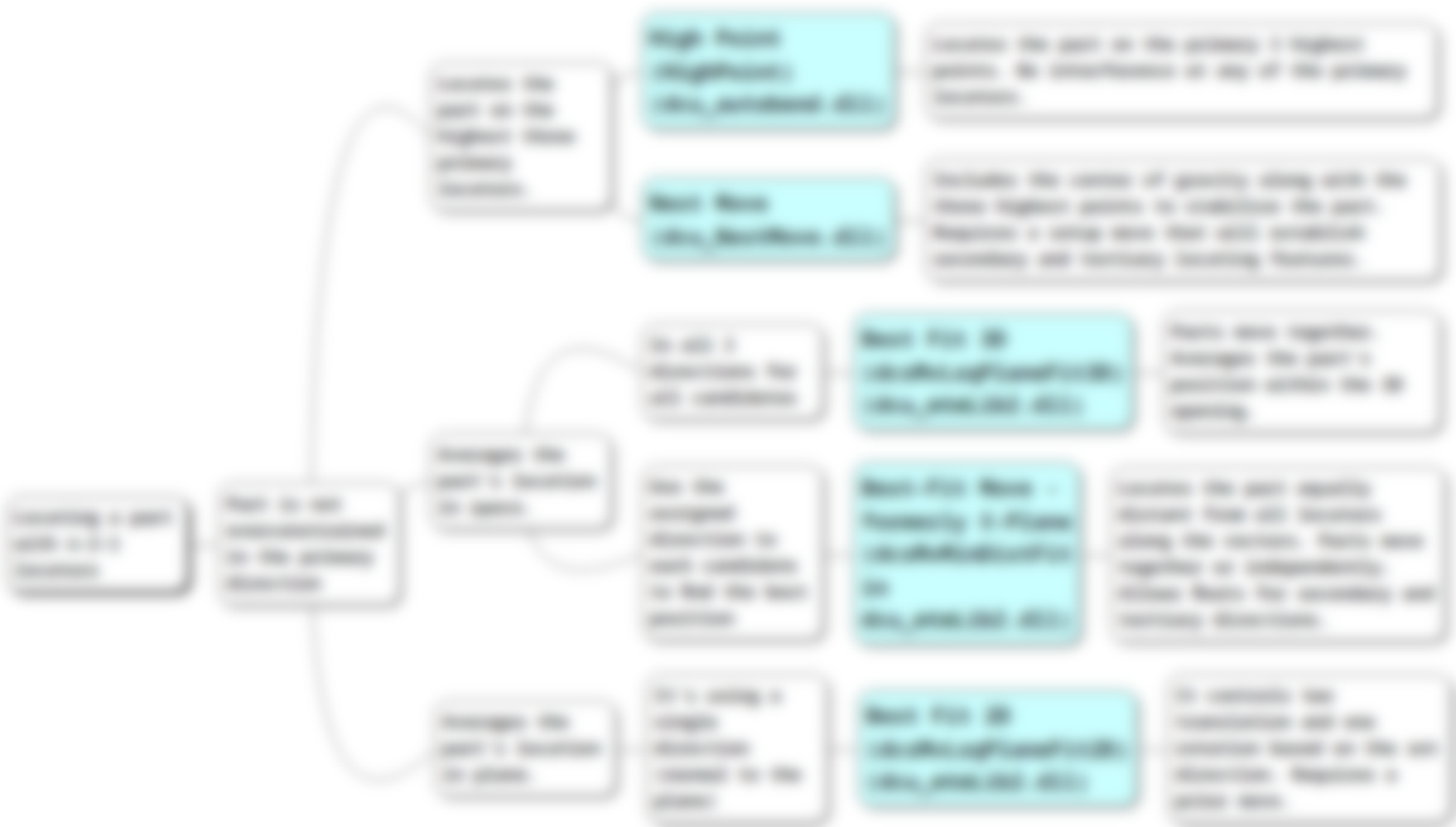
3DCS Variation Analyst is a CAD-based simulation software that determines the risk of failure in production and the amount of variation expected from a given design when manufactured. Using Monte Carlo Analysis to simulate the Digital Twin, 3DCS provides the most advanced tolerance analysis tool on the market.
3DCS Variation Analyst offers users the ability to do more than just 3D stack-ups by analyzing the relationship between your parts and accounting for a multitude of sources of variation. This gives you the most accurate results to make important decisions about your design and manufacturing processes.
